Bob là một nhân viên cứu hộ bờ biển tại thành phố Nha Trang xinh đẹp. Ngày hôm nay, trong lúc anh ta đang trực cứu hộ, anh ấy thấy một người đàn ông say rượu bị nước cuốn và chìm xuống dưới biển. Giả sử bãi biển là một mặt phẳng Euclid và đường bờ biển là đường y = 0. Các vị trí phía trên bờ biển nằm phía trên đường y=0 còn các vị trí dưới biển nằm ở phía dưới đường y=0. Tốc độ của Bob trên đất liền là v1 và tốc độ khi anh ấy bơi là v2.

Giả sử hiện tại Bob đang đứng ở vị trí có tọa độ (x1, y1) và người đàn ông bị chìm ở vị trí có tọa độ (x2, y2). Bob cần thời gian tối thiểu là bao lâu để tới được vị trí người đàn ông bị chìm và cứu anh ta.

Dữ liệu vào:

• Dòng đầu tiên chứa một số nguyên dương T (1 <= T <= 100) – là số testcase;

• T dòng tiếp theo, mỗi dòng chứa 6 số nguyên x1, y1, x2, y2, v1, v2 (~-10^9~ <= x1, x2 <= ~10^9~; ~-10^9~ <= y1 < 0; 0 < y2, v1, v2 <= ~10^9~) mỗi số cách nhau một dấu cách

Dữ liệu ra:

Với mỗi testcase đưa ra thời gian tối thiểu cần thiết với đúng 5 chữ số sau dấu thập phân.

Ví dụ:

Dữ liệu vào:

1

3 -20 3 25 40 5

Dữ liệu ra

5.50000

Hai người đàn ông đang di chuyển đồng thời, một người đang di chuyển từ A đến B và người kia đang di chuyển từ C đến D. Ban đầu người thứ nhất ở A, và người thứ hai ở C. Họ duy trì vận tốc không đổi sao cho khi người thứ nhất đến B, thì cùng lúc đó người thứ hai đến D. Bạn có thể cho rằng A, B, C và D là tọa độ Descartes 2D. Bạn phải tìm khoảng cách Euclidean nhỏ nhất giữa hai người đàn ông khi di chuyển trên đường đi.

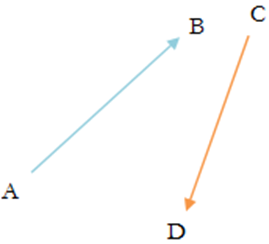
Dữ liệu vào:

• Dòng đầu tiên chứa một số nguyên dương T T (≤ 1000) – số testcase;
• T dòng tiếp theo, mỗi dòng chứa 8 số nguyên dương Ax, Ay, Bx, By, Cx, Cy, Dx, Dy. Tất cả các tọa độ đều nằm trong khoảng từ 0 đến 100. Trong đó (Ax, Ay) biểu diễn tọa độ điểm A, (Bx, By) biểu diễn tọa độ điểm B, (Cx, Cy) biểu diễn tọa độ điểm C và (Dx, Dy) biểu diễn tọa độ điểm D.

Dữ liệu ra:

*Đối với mỗi testcase, in ra khoảng cách tối thiểu giữa hai người đàn ông khi di chuyển trên đường đi của họ.

Ví dụ:

Dữ liệu vào:

2
21 69 34 58 47 80 67 63
28 96 7 0 64 13 82 77

Dữ liệu ra:

Case 1: 28.2311884270
Case 2: 54.6317196562

Hoàng là một chuyên gia về xử lý dữ liệu. Một ngày đẹp trời, cậu ta nhận được nguồn dữ liệu tử một người bạn đề nghị Hoàng xử lý giúp dữ liệu cho họ. Khi tiến hành kiểm tra nguồn dữ liệu nhận được, Hoàng nhận thấy dữ liệu đã cho còn thiếu một bộ dữ liệu nữa thì mới trở thành dữ liệu hoàn chỉnh.

Đồng chí hãy giúp Hoàng tìm dữ liệu còn thiếu trong bộ dữ liệu nhận được.

Dữ liệu vào:

• Dòng đầu tiên chứa một số nguyên dương N (2 <= N <= ~10^9~);
• Dòng tiếp theo chứa N số nguyên dương a1, a2, …, aN (1 <= ai ,+ ~10^9~; ai < ai+1) mỗi số cách nhau một dấu cách.

Dữ liệu ra:

In ra các số còn thiếu tìm được.

Ví dụ:

Dữ liệu vào:

6
2 4 8 10 12 14

Dữ liệu ra:

6

Cho 2 số nguyên b (b>1) và n (n>0), Thực hiện phép toán f(b,n) và được định nghĩa như sau:

• f(b,n) = n nếu n < b
• f(b,n) =f(b,floor(n/b)) + (n mod b) nếu n>=b

Trong đó floor(n/b) biểu thị số nguyên lớn nhất không vượt quá n/b và n mod b biểu thỉ phép chia module n cho b.

Ví dụ:

• f(10,87654)=8+7+6+5+4=30
• f(100,87654)=8+76+54=138

Đầu vào:

là số nguyên n và chuỗi s (1≤n≤~10^{11}~; 1≤s≤~10^{11}~) cách nhau 1 khoảng trắng

Đầu ra:

in ra kết quả phép tổng s nếu có, ngược lại in ra -1

Ví dụ:

Input

87654 30

Output

10

Trong một trường học có n lớp (mỗi lớp gồm cả nam lẫn nữ). Lớp học i có ~a_i~ thành viên. Tất cả trường đi du lịch bằng xe du lịch, các xe được bố trí có r hàng ghế và mỗi hàng ghế 2 bạn ngồi. Hạnh phúc nhất là khi:

• Một thành viên khác trong lớp ngồi cùng hàng với họ, hoặc
• Họ ngồi một mình trong hàng của họ (có một ghế trống bên cạnh).

Xác định số lượng người vui vẻ tối đa trong cách sắp xếp chỗ ngồi tối ưu. Lưu ý rằng mọi người phải ngồi trên chuyến xe buýt. Đảm bảo rằng tất cả các thành viên trong lớp sẽ ngồi vừa trên xe buýt. ~\sum_{i=1}^{n}a_{i} ≤ 2r~

Đầu vào:

• gồm t dòng (1 ≤ t ≤ ~10^5~)
• Dòng thứ nhất gồm 2 số n và r (1 ≤ n ≤ 100; 1 ≤ r≤ 500)
• Dòng tiếp theo chứa n số nguyên ~a_1, a_2, .., a_n~ (1 ≤ ~ a_i~ ≤ 10)

Đầu ra:

Hãy đưa ra số lượng người vui vẻ tối đa trong cách sắp xếp chỗ ngồi tối ưu tương ứng với mỗi bộ test

Ví dụ:

Input

4
3 3
2 3 1
3 3
2 2 2
4 5
1 1 2 2
4 5
3 1 1 3

Output

4
6
6
6